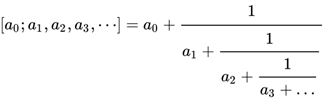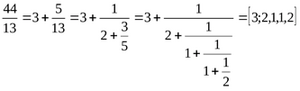Сетевой проект В мире ломаных чисел/Цепные дроби

Участие в проекте О проекте Распоряжение о проведении Положение о проекте РЕГИСТРАЦИЯ УЧАСТНИКОВ Информационный навигатор Сетевые ресурсы Информация для родителей Форум проекта Этапы проекта - Общий знаменатель - Дроби древнего мира - Numeri fracti по-русски - Цепные дроби - Викторина в проекте Рейтинг участников Слово жюри Доска объявлений 20 Авторы и координаторы проекта Пчелинцева Татьяна Александровна, заслуженный учитель Российской Федерации, методист Центра поддержки одаренных детей "Платформа 33" ГАОУ ДПО ВО ВИРО (г.Владимир) Тел. +7(4922) 77-85-99 E-mail: pchelintsewata@yandex.ru Львова Алла Геннадьевна, учитель математики и информатики высшей квалификационной категории (Судогодский район), методист ГАОУ ДПО ВО ВИРО (г.Владимир) М.тел. 89157642232 Лопаткина Елена Вячеславовна, канд. пед. наук, доцент кафедры физико-математического образования и ИТ Педагогического института ВлГУ (г.Владимир). В МИРЕ ЛОМАНЫХ ЧИСЕЛ Сроки этапа: 13 марта 2023 г. - 28 марта 2023 г. "Хотя этот род выражений до настоящего времени разработан мало, однако мы не сомневаемся, что когда-нибудь применение его весьма широко распространится в анализе бесконечных" Леонард Эйлер (1707-1783), швейцарский, прусский и российский математик и механик Термин «цепная дробь» («Kettenbruche») появился в Германии в середине XVIII в., а Леонард Эйлер приблизительно в это же время назвал такие дроби «непрерывными» («Continue fraction»). Английский математик Джон Валлис тоже использовал термин «непрерывные дроби» в своей книге “Arithmeticain fon itorium” (“Арифметика бесконечных”), которая вышла в 1655 г. Так за этими дробями и сохранились оба названия. Обычно “цепные дроби” и “непрерывные дроби” рассматриваются как синонимы. Простейшей цепной дробью называется выражение вида (где а0 может быть любым числом, а1,а2, … - положительные числа): В виде цепной дроби можно записать не только обыкновенную дробь, но и любое действительное число. Современное обозначение непрерывных дробей предложил выдающийся нидерландский учёный Христиан Гюйгенс (1629-1695). В 1680 г. он был вынужден обратиться к цепным дробям при построении планетария в Париже. Детальное изучение теории цепных дробей помогло ученому правильно подобрать число зубцов используемых в планетарии шестерен, демонстрирующих движение планет: отношения периодов обращения планет и отношения числа зубцов взаимосвязанных между собой шестерен планетария должны были совпадать. В истории математического образования было время, когда теорию цепных дробей изучали в средней школе. Но в настоящее время она исключена из программы. Как получить цепную дробь из обыкновенной дроби, где она применяется, кто из советских и российских учёных занимался вопросами цепных дробей? Поиску ответов на эти вопросы будет посвящен четвёртый этап нашего проекта. Проектное задание Изучите историю появления и развития понятия «цепная дробь» от момента её появления и до наших дней. Составьте хронологическую таблицу по результатам своих изысканий. Отметьте на интерактивной карте мира имена ученых, которые внесли свой вклад в развитие понятия «цепная дробь» Изучите жизнь и научную деятельность замечательного математика, удивительного изобретателя и конструктора Христиана Гюйгенса: составьте биографическую таблицу, отражающую основные события из жизни ученого; составьте перечень научных работ Гюйгенса в календарной последовательности Назовите имена советских и русских учёных, занимающихся вопросами цепных дробей; дайте краткое описание их вклада. Технологии выполнения задания сетевой сервис для создания виртуальных досок Padlet (шаблон КАРТА), как работать с сервисом - ЗДЕСЬ конструктор сайтов Tilda Publishing: - инструкция от пользователей - ЗДЕСЬ - инструкции по редактированию от разработчиков - ЗДЕСЬ: как сделать многостраничный сайт; берем самое основное - советы, как работать с текстом и графикой при оформлении сайта проверка на "Антиплагиат" Критерии оценки представленных работ: Содержание разделов сайта: на четвертой странице авторского сайта (ЦЕПНЫЕ ДРОБИ): опубликована таблица, отражающая историю появления и развития понятия «цепная дробь» от момента её появления и до наших дней; в таблице в хронологической последовательности приведены данные: имя ученого с указанием хронологических данных, страна, вклад в развитие понятия, научная работа (если возможно ее указать), в которой рассматриваются цепные дроби, их свойства, применение, дополнительная информация по теме проектного задания - до 2  баллов за каждое имя, но не более 30 баллов опубликована ссылка на интерактивную карту; каждая интерактивная метка на карте содержит: заголовок метки - имя ученого, хронологические данные , указание страны проживания, графический и/или звуковой объект - до 1  балла за каждую метку, но не более 15 баллов опубликована биографическая таблица, наиболее полно отражающая основные события из жизни и научной деятельности Христиана Гюйгенса - до 5  баллов опубликован перечень научных работ Христиана Гюйгенса (в календарной последовательности) -  до 3  баллов опубликован иллюстрированный пост, посвященный отечественным ученым, чьи имена связаны с изучением цепных дробей; отмечен вклад каждого из них - до 2  баллов за каждое имя, но не более 20 баллов Оформление страницы сайта: использование единого стиля на всех блоках страницы - до 2  баллов используемая навигация обеспечивает доступность и удобство восприятия информации: - наличие ссылки на страницу в главном меню сайта -  1  балл - наличие ссылок на отдельные блоки (посты) внутри страницы - до 2  баллов соответствие художественного оформления страниц размещенной на них информации - до 3  баллов сбалансированность цветовой схемы, шрифтов и графики - до 3  баллов использование визуальных эффектов, в т.ч. затемнений, наложений, эффекта параллакса - до 3  баллов Бонусы: бонус за содержание - до 3  баллов бонус за оформление - до 3 баллов Максимальное количество баллов  - 93