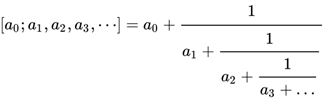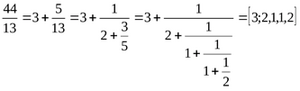Сетевой проект В мире ломаных чисел/Цепные дроби: различия между версиями
| Строка 2: | Строка 2: | ||
<div align="center"><div style="background-color:#fedcd2; color: #527590"> <font size="4"><p>Сроки этапа:<font size="4" color="#ff0000"><b> 10 марта 2023 г. - 25 марта 2023 г.</b></font></p></font></div>__NOTOC__ | <div align="center"><div style="background-color:#fedcd2; color: #527590"> <font size="4"><p>Сроки этапа:<font size="4" color="#ff0000"><b> 10 марта 2023 г. - 25 марта 2023 г.</b></font></p></font></div>__NOTOC__ | ||
<div align="justify"> | <div align="justify"> | ||
{|align="justify" cellpadding="0" cellspacing="0" style="margin-left:1em" width="70%" | |||
|- | |||
|[[Файл:Академик_Леонард_Эйлер.jpg|250x250 px|]] | |||
|<blockquote><i><p align="left"> <i> | |||
"Хотя этот род выражений до настоящего времени разработан мало, однако мы не сомневаемся, что когда-нибудь применение его весьма широко распространится в анализе бесконечных" | |||
</i> <p align="right"> Леонард Эйлер (1707-1783), швейцарский, прусский и российский математик и механик | |||
</p></blockquote> | |||
|} | |||
<p align="justify"> | |||
Термин <i>«цепная дробь» («Kettenbruche»)</i> появился в Германии в середине XVIII в., а Леонард Эйлер приблизительно в это же время назвал такие дроби <i>«непрерывными» («Continue fraction»)</i>. Английский математик [https://ru.wikipedia.org/wiki/Валлис,_Джон Джон Валлис] тоже использовал термин «непрерывные дроби» в своей книге “Arithmeticain fon itorium” (“Арифметика бесконечных”), которая вышла в 1655 г.<br> | |||
Так за этими дробями и сохранились оба названия. Обычно “цепные дроби” и “непрерывные дроби” рассматриваются как синонимы. <br> | |||
{|align="justify" cellpadding="0" cellspacing="0" style="margin-left:1em" width="68%" | |||
|- | |||
|<i><font color="#A60000">Простейшей цепной дробью называется выражение вида (где а0 может быть любым числом, а1,а2, … - положительные числа):</font></i> | |||
| | |||
|[[Файл:Цепь.png|350px|справа]] | |||
|} | |||
{|align="justify" cellpadding="0" cellspacing="0" style="margin-left:1em" width="68%" | |||
|- | |||
|[[Файл:Цепь2.png|300px|слева]]<i><font color="527590">В виде цепной дроби можно записать не только обыкновенную дробь, но и любое действительное число.</font></i><br> | |||
|- | |||
|[[Файл:Christiaan_Huygens-painting.jpeg|200px|справа]]Современное обозначение непрерывных дробей предложил выдающийся нидерландский учёный [https://ru.wikipedia.org/wiki/Гюйгенс,_Христиан Христиан Гюйгенс (1629-1695)]. В 1680 г. он был вынужден обратиться к цепным дробям при построении планетария в Париже. Детальное изучение теории цепных дробей помогло ученому правильно подобрать число зубцов используемых в планетарии шестерен, демонстрирующих движение планет: отношения периодов обращения планет и отношения числа зубцов взаимосвязанных между собой шестерен планетария должны были совпадать.<br> | |||
|} | |||
В истории математического образования было время, когда теорию цепных дробей изучали в средней школе. Но в настоящее время она исключена из программы. <br> | |||
<b><i>Как получить цепную дробь из обыкновенной дроби, где она применяется, кто из советских и российских учёных занимался вопросами цепных дробей?</i></b> <br> | |||
Поиску ответов на эти вопросы будет посвящен четвёртый этап нашего проекта.<br> | |||
{| width="70%" cellpadding= "2" cellspacing="5" style="vertical-align:top; background:#FFFFFF;" | |||
!<div style="border: 1px solid #a3b0bf; -moz-border-radius: 10px; padding: 5px; margin: 0px 0px 0px 0px; background: #cedff2; text-align:left; color:#A62A00; text-size:20px; padding:0.2em 0.4em;">Проектное задание</div> | |||
|} | |||
<div align="justify"> | |||
---- | |||
Версия 19:57, 7 февраля 2023
|
Участие в проекте
Этапы проекта
Авторы и координаторы проекта
Пчелинцева Татьяна Александровна, заслуженный учитель Российской Федерации, методист ЦПОД "Платформа Владимир" ГАОУ ДПО ВО ВИРО
Тел. +7(4922) 77-85-99 Львова Алла Геннадьевна, учитель математики и информатики высшей квалификационной категории (Судогодский район), методист ЦПОД "Платформа Владимир" ГАОУ ДПО ВО ВИРО
М.тел. 89157642232 Лопаткина Елена Вячеславовна, канд. пед. наук, доцент кафедры физико-математического образования и ИТ Педагогического института ВлГУ (г.Владимир).
Сроки этапа: 10 марта 2023 г. - 25 марта 2023 г.
Термин «цепная дробь» («Kettenbruche») появился в Германии в середине XVIII в., а Леонард Эйлер приблизительно в это же время назвал такие дроби «непрерывными» («Continue fraction»). Английский математик Джон Валлис тоже использовал термин «непрерывные дроби» в своей книге “Arithmeticain fon itorium” (“Арифметика бесконечных”), которая вышла в 1655 г.
В истории математического образования было время, когда теорию цепных дробей изучали в средней школе. Но в настоящее время она исключена из программы.
|