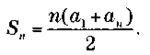Сетевой проект Закон и порядок: удивительный мир прогрессий/Арифметическая прогрессия
Тел. +7(4922) 77-85-99
М.тел. 89157642232
ЗАКОН И ПОРЯДОК:
УДИВИТЕЛЬНЫЙ МИР ПРОГРЕССИЙ
Сроки этапа: 21 февраля 2022 г. - 07 марта 2022 г.
Третий этап нашего проекта посвящен одному из величайших математиков всех времён, «королю математики» Карлу Фридриху Гауссу.
Величайший немецкий математик, астроном и физик Карл Гаусс родился в городе Брауншвейг (Германия). Его отец, садовник и фонтанный мастер, славился искусством быстро и легко считать. Эта способность перешла к сыну, говорившему позднее, что он «умел считать раньше, чем говорить».
Известна история, из которой видно, насколько легко давались Гауссу арифметические вычисления. Когда мальчику было 9 лет, школьный учитель Бюттнер предложил своим ученикам сложить 100 первых натуральных чисел, будучи уверенным в том, что это займет класс достаточно долго, а он в это время сможет отдохнуть. И вот в то время как остальные ученики едва приступили к заданию, Гаусс уже положил свою доску на стол учителя, воскликнув: Ligget se! («Вот оно!»). Бюттнер подумал, что Гаусс просто дерзит ему, но когда он посмотрел на доску, то обнаружил, что на ней записан правильный ответ — 5050, причем не было приведено ни одного этапа вычислений.
|
История о сумме 100 первых натуральных чисел и общая формула, которую мы знаем как сумму n первых членов арифметической прогрессии, необходимы для введения в тему, которой Гаусс посвятил много времени в молодости. Одним из величайших трудов математика стала книга Disquisitiones arithmeticae («Арифметические исследования»), увидевшая свет в 18001 г. В «Исследованиях» Гаусс придал новое направление теории чисел, которая перестала быть набором разрозненных результатов и превратилась в важную математическую дисциплину. Удивительно, что все изложенные в книге результаты были получены Гауссом в возрасте до 30 лет!
В чем заключается вклад Гаусса в теорию чисел? Что знали современники Гаусса об арифметической прогрессии и что им еще предстояло узнать? В каком направлении идет изучение последовательностей, родственных арифметической прогрессии, в современной математике? Надеемся, поиск ответов на эти вопросы откроет нашим участникам пока неизвестные им страницы истории математики.
Проектное задание
|
|---|
- Изучите жизнь Карла Фридриха Гаусса и его научные достижения в области теории чисел
- Создайте онлайн-газету, посвященную самым ярким, на ваш взгляд, страницам жизни Гаусса и его величайшему труду Disquisitiones arithmeticae
- Выясните, в работах каких ученых и в каких древних задачах обнаруживается арифметическая прогрессия? В каких областях, помимо математики, можно ее встретить? Подтвердите каждый случай наглядным примером
- Определите, в каком направлении развивается современное исследование прогрессий
- Опубликуйте результаты исследования на сайте [...]; разместите ссылку на своей странице
Технологии выполнения задания
|
|---|
|
Критерии оценки представленных работ:
|
|---|
- Содержание Ленты времени, отражающей биографию и научную деятельность Леонардо Пизанского:
- на Ленте времени представлены не менее 5 хронологических меток: каждая метка имеет хронологический заголовок (дата или период), представлена постом, имеющим заголовок и содержащим лаконичный авторский текст по теме проектного задания - до 2 баллов за метку, но не более 20 баллов;
- информативность Ленты (отражение наиболее значимых событий в жизни математика) - до 3 баллов
- отражение особого вклада Леонардо Пизанского в развитие математики - до 3 баллов
- Определены основные свойства, которыми обладает числовая последовательность чисел Фибоначчи - до 2 баллов за свойство, но не более 40 баллов;
- Описаны ситуации, в которых обнаруживаются последовательности чисел Фибоначчи:
- в различных средах окружающего мира - 1 балл за каждый пример, но не более 10 баллов;
- в текстовых математических задачах - до 5 баллов
- По результатам работы создан и размещен на одном из облачных сервисов (Яндекс.Диск, Мail.Ru) pdf-документ; ссылка на документ опубликована на странице участника - 1 балл
- Оформление Ленты времени:
- читабельность текста (с минимумом встроенных в текст гиперссылок) для каждой метки - до 3 баллов
- оптимальное использование разнообразных медиаресурсов (графических (фотографий, рисунков, репродукций, карт), видео) - до 5 баллов
- ссылки на первоисточник (интерактивное название сайта; название библиографического издания с указание автора, издательства, года издания и используемых страниц)- до 2 баллов
- эстетичность Ленты - до 3 баллов
- Оформление раздела "Свойства чисел Фибоначчи":
- использование единого стиля во всех фрагментах текста или слайдах слайд-шоу - до 2 баллов
- качество математического текста (научная строгость оформления, читабельность текста) - до 5 баллов
- Оформление раздела "Числа Фибоначчи вокруг нас":
- использование единого стиля во всех фрагментах текста или слайдах слайд-шоу - до 2 баллов
- оптимальное использование разнообразных медиаресурсов (графических (фотографий, рисунков, репродукций, карт), видео) - до 5 баллов
- качество математического текста (научная строгость оформления, читабельность текста) - до 5 баллов
- Используемая навигация обеспечивает доступность и удобство восприятия информации - до 3 баллов
- Бонус за содержание - до 5 баллов
- Бонус за оформление - до 3 баллов